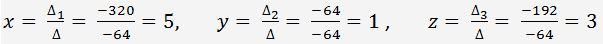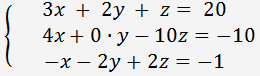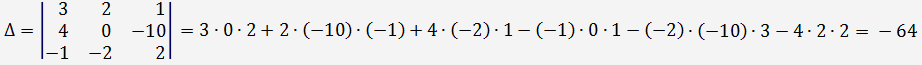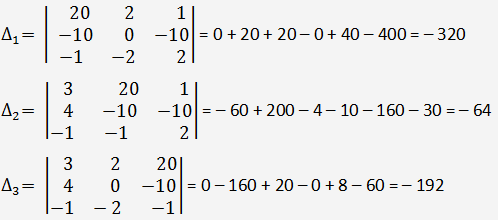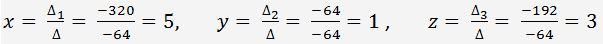Επίλυση συστημάτων τριών γραμμικών εξισώσεων σε τρεις μεταβλητές
Συστήματα τριών γραμμικών εξισώσεων με τρεις μεταβλητές 3x3
a
11x
1 + a
12x
2 + a
13x
3 = b
1
a
21x
1 + a
22x
2 + a
23x
3 = b
2
a
31x
1 + a
32x
2 + a
33x
3 = b
3
όπου x
1, x
2, x
3 είναι τα άγνωστα, a
11,..., a
33 είναι οι συντελεστές του συστήματος, b
1, b
2, b
3 είναι οι σταθερές τιμές.
Υπολογιστής για σύστημα γραμμικών εξισώσεων
Αυτή η δωρεάν ηλεκτρονική αριθμομηχανή μπορεί να χρησιμοποιηθεί για την επίλυση συστημάτων τριών γραμμικών εξισώσεων με τρεις μεταβλητές.
Για να λύσετε ένα σύστημα γραμμικών εξισώσεων χρησιμοποιώντας την ηλεκτρονική αριθμομηχανή, εισαγάγετε τους συντελεστές των τριών γραμμικών εξισώσεων και πατήστε 'Επίλυση'.
Πώς να λύσετε ένα σύστημα τριών γραμμικών εξισώσεων σε τρεις μεταβλητές χρησιμοποιώντας τον κανόνα του Cramer
Παράδειγμα. Λύστε το σύστημα τριών γραμμικών εξισώσεων σε τρεις μεταβλητές χρησιμοποιώντας
τον κανόνα του Cramer's.
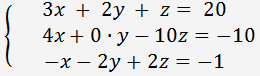
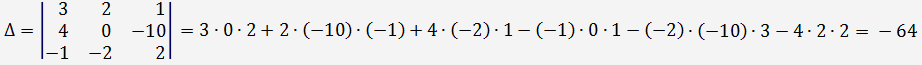
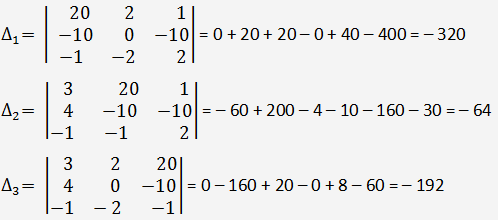
Με τον κανόνα του Cramer: